Hi @vperetroukhin,
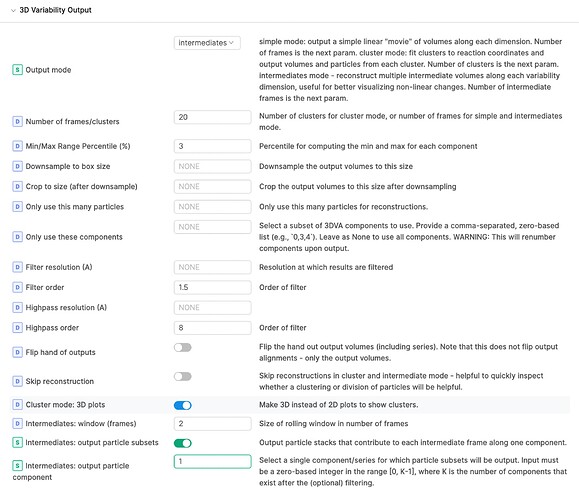
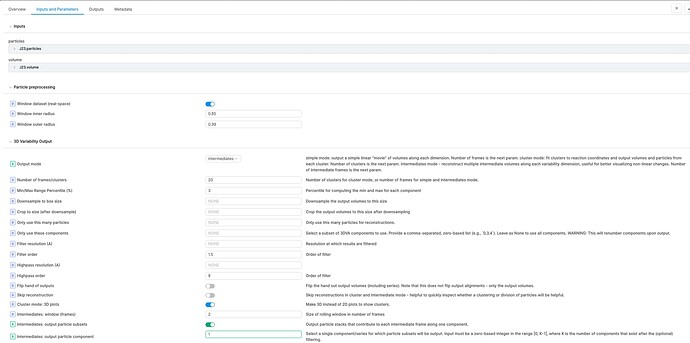
In my 3DVA Display job (cryoSPARC v3.3.1) with Output mode of intermediates, I enabled “Intermediates: output particle subsets” and set 1 for “Intermediates: output particle component”. However, I could not see “output particle subsets”. All other parameters are in default. Did I miss something? Thanks!
Here is the partial log:
Compiling job outputs…
[CPU: 7.27 GB] Passing through outputs for output group particles_series_1_frame_0 from input group particles
[CPU: 7.27 GB] This job outputted results [‘blob’]
[CPU: 7.27 GB] Loaded output dset with 0 items
[CPU: 7.27 GB] Passthrough results [‘ctf’, ‘alignments3D’, ‘components_mode_0’, ‘components_mode_1’, ‘components_mode_2’, ‘components_mode_3’, ‘components_mode_4’, ‘components_mode_5’, ‘components_mode_6’]
[CPU: 11.93 GB] Loaded passthrough dset with 742501 items
[CPU: 10.49 GB] Intersection of output and passthrough has 0 items
[CPU: 10.49 GB] Passing through outputs for output group particles_series_1_frame_1 from input group particles
[CPU: 10.49 GB] This job outputted results [‘blob’]
[CPU: 10.49 GB] Loaded output dset with 0 items
[CPU: 10.49 GB] Passthrough results [‘ctf’, ‘alignments3D’, ‘components_mode_0’, ‘components_mode_1’, ‘components_mode_2’, ‘components_mode_3’, ‘components_mode_4’, ‘components_mode_5’, ‘components_mode_6’]
[CPU: 11.93 GB] Loaded passthrough dset with 742501 items
[CPU: 10.49 GB] Intersection of output and passthrough has 0 items
[CPU: 10.49 GB] Passing through outputs for output group particles_series_1_frame_2 from input group particles
[CPU: 10.49 GB] This job outputted results [‘blob’]
[CPU: 10.49 GB] Loaded output dset with 0 items
[CPU: 10.49 GB] Passthrough results [‘ctf’, ‘alignments3D’, ‘components_mode_0’, ‘components_mode_1’, ‘components_mode_2’, ‘components_mode_3’, ‘components_mode_4’, ‘components_mode_5’, ‘components_mode_6’]
[CPU: 11.93 GB] Loaded passthrough dset with 742501 items
[CPU: 10.49 GB] Intersection of output and passthrough has 0 items
[CPU: 10.49 GB] Passing through outputs for output group particles_series_1_frame_3 from input group particles
[CPU: 10.49 GB] This job outputted results [‘blob’]
[CPU: 10.49 GB] Loaded output dset with 0 items
[CPU: 10.49 GB] Passthrough results [‘ctf’, ‘alignments3D’, ‘components_mode_0’, ‘components_mode_1’, ‘components_mode_2’, ‘components_mode_3’, ‘components_mode_4’, ‘components_mode_5’, ‘components_mode_6’]
[CPU: 11.94 GB] Loaded passthrough dset with 742501 items
[CPU: 10.49 GB] Intersection of output and passthrough has 0 items
[CPU: 10.49 GB] Passing through outputs for output group particles_series_1_frame_4 from input group particles
[CPU: 10.49 GB] This job outputted results [‘blob’]
[CPU: 10.49 GB] Loaded output dset with 0 items
[CPU: 10.49 GB] Passthrough results [‘ctf’, ‘alignments3D’, ‘components_mode_0’, ‘components_mode_1’, ‘components_mode_2’, ‘components_mode_3’, ‘components_mode_4’, ‘components_mode_5’, ‘components_mode_6’]
[CPU: 11.94 GB] Loaded passthrough dset with 742501 items
[CPU: 10.49 GB] Intersection of output and passthrough has 0 items
[CPU: 10.49 GB] Passing through outputs for output group particles_series_1_frame_5 from input group particles
[CPU: 10.49 GB] This job outputted results [‘blob’]
[CPU: 10.49 GB] Loaded output dset with 0 items
[CPU: 10.49 GB] Passthrough results [‘ctf’, ‘alignments3D’, ‘components_mode_0’, ‘components_mode_1’, ‘components_mode_2’, ‘components_mode_3’, ‘components_mode_4’, ‘components_mode_5’, ‘components_mode_6’]
[CPU: 11.93 GB] Loaded passthrough dset with 742501 items
[CPU: 10.49 GB] Intersection of output and passthrough has 0 items
[CPU: 10.49 GB] Passing through outputs for output group particles_series_1_frame_6 from input group particles
[CPU: 10.49 GB] This job outputted results [‘blob’]
[CPU: 10.49 GB] Loaded output dset with 0 items
[CPU: 11.94 GB] Loaded passthrough dset with 742501 items
[CPU: 10.49 GB] Intersection of output and passthrough has 0 items
…
[CPU: 10.49 GB] Checking outputs for output group particles_series_1_frame_0
[CPU: 10.49 GB] Checking outputs for output group particles_series_1_frame_1
[CPU: 10.49 GB] Checking outputs for output group particles_series_1_frame_2
[CPU: 10.49 GB] Checking outputs for output group particles_series_1_frame_3
[CPU: 10.49 GB] Checking outputs for output group particles_series_1_frame_4
[CPU: 10.49 GB] Checking outputs for output group particles_series_1_frame_5
[CPU: 10.49 GB] Checking outputs for output group particles_series_1_frame_6
[CPU: 10.49 GB] Checking outputs for output group particles_series_1_frame_7
[CPU: 10.49 GB] Checking outputs for output group particles_series_1_frame_8
[CPU: 10.49 GB] Checking outputs for output group particles_series_1_frame_9
[CPU: 10.49 GB] Checking outputs for output group particles_series_1_frame_10
[CPU: 10.49 GB] Checking outputs for output group particles_series_1_frame_11
[CPU: 10.49 GB] Checking outputs for output group particles_series_1_frame_12
[CPU: 10.49 GB] Checking outputs for output group particles_series_1_frame_13
[CPU: 10.49 GB] Checking outputs for output group particles_series_1_frame_14
[CPU: 10.49 GB] Checking outputs for output group particles_series_1_frame_15
[CPU: 10.49 GB] Checking outputs for output group particles_series_1_frame_16
[CPU: 10.49 GB] Checking outputs for output group particles_series_1_frame_17
[CPU: 10.49 GB] Checking outputs for output group particles_series_1_frame_18
[CPU: 10.49 GB] Checking outputs for output group particles_series_1_frame_19
[CPU: 10.49 GB] Updating job size…
[CPU: 10.49 GB] Exporting job and creating csg files…
[CPU: 10.50 GB] ***************************************************************
[CPU: 10.50 GB] Job complete.