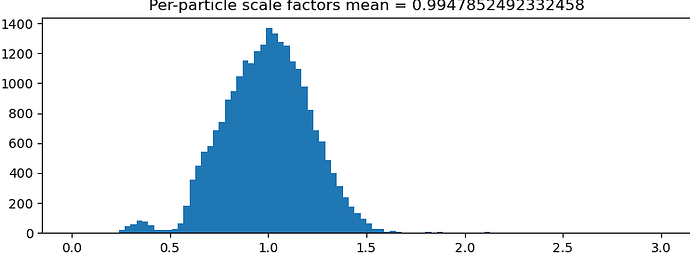
Hi All, I run a NU Refinement (New) with the option “minimize over per-particle scale” on, and I got a wide distribution range for the per-particle scale factors as in the attached picture. For example, if the per-particle scale factor is 1.5, does that mean the corresponding particle is 50% off in size (which seems something wrong because the particles should not change that much in size)? Thanks!
My understanding is that the scale factors pertain more to contrast than size
Hi @donghuachen,
The particle scale-factor is there in order to correct for contrast differences, as Oli pointed out. The primary reason this is useful is when ice thickness varied quite a bit during data collection: this affects the relative contrast of the protein against the solvent background, so a multiplicative scale helps correct for this. In your example, particles that have a scale factor of 1.5 are weighted 1.5 times as much as the mean particle is during refinement.
Best,
Michael
Hi @olibclarke @mmclean,
Thanks for your explanation!
I thought it was the magnification calibration for each particle. Is there any option in cryosparc doing this magnification correction for each particle? Maybe I have missed it.
Hi @donghuachen,
There isn’t support for significant per-particle magnification correction. Generally this would only be needed when merging datasets of two different pixel sizes; see Ali’s discussion on this topic. If you combined two datasets with two different pixel sizes, it’s generally recommended to process each dataset individually, since often times only one dataset will contribute high resolution information.
Otherwise, if working with micrographs taken at one pixel size, your initial comment is right – you generally only expect to see small magnification discrepancies. So for small magnification discrepancies that are constant over the dataset (e.g. due to microscope anisotropy), there will be an option to estimate and correct for this in the next release of cryoSPARC. The method is described in Zivanov et al. 2020 in section 2.4. The method was developed to correct for anisotropic magnification, and so can only correct for discrepancies of a few percent. But note that this is a global correction – magnification parameters are assumed to be constant for each exposure group, and this is necessary because signal must be aggregated over many particles to estimate for anisotropic magnification. There is no method that I know of that can estimate for individual particle magnifications. The only other thing that comes to mind is estimating per-particle defocus, but I am not too sure if defocus has a measurable effect on particle magnifications.
Best,
Michael
Hi @mmclean,
Thanks for your details.
It would be great to have the anisotropic magnification correction and also the ability to merge datasets with different pixel sizes in cryosparc.
@mmclean per particle correction of anisotropic magnification actually exists in JSPR (An Algorithm for Estimation and Correction of Anisotropic Magnification Distortion of Cryo-EM Images without Need of Pre-calibration - PMC), although I am not aware of widespread use, and I haven’t looked in detail as to how it works.
@mmclean I believe magnification varies with defocus for non-parallel beam. I don’t know the formula, though.
Interesting, thanks for bringing this to my attention – I’ll have to look into it! Totally missed this when looking through the literature.
Best,
Michael
It seems the relation between defocus-dependent magnification variation and non-parallelism depends on the particular objective lense configuration - though for sure the variation can be pretty significant when the beam isn’t nicely parallel. I found some empirical tests on the page below. Pretty interesting (not the difference between over and underfocus at 50,000X).