I met a problem that the 3D refined map have two preferred orientations.
Maybe the Rebalance 2D Classification job will be a good method to solve the question. But I wanted to know the relationship between ‘3dalignment/pose’ and ‘angular direction distribution: azimuth/elevation’. How can I calculate or transform these two things? Were there any existed scripts or guidelines? What I wanted to do was to remove duplicate particles based on the angular direction distribution.
For example, in the following picture, some points had 10^4 particles while some points had tens of particles. If I can remove some particles which was on the point of very red, maybe it could be very easy to resolve the preferred orientation problem.
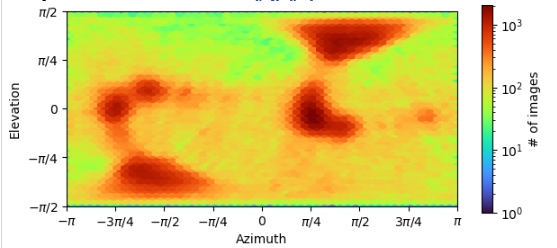
Looks to me like a bit of an orientation bias (or a few of them) rather than a preferred single orientation. I would be a little surprised if a distribution like this led to a very distorted map. However, if the particles are misaligned, then the distribution plot isn’t trustworthy either. You can try doing more 3D classification, or doing a reconstruction in cisTEM (often this fixes minor preferred orientation distortions because of the volume filter it uses).
The alignment poses in cryoSPARC are Rodrigues axis-angle vectors if you want to play with them yourself.
I was agree with you about the angular distribution affecting the preferred orientations. I had attempted to do further 3D classification which could take apart of different orientations in different classes. Maybe it was a little amazing.
Heterogeneous Refinement parameters:
(The others were default)
Classes: 5
Bin: 1
Initial resolution: 60
Assignment convergence criteria: 0.02
Number of final full iterations: 5
Btw, I really wanted to work out the relationship between ‘3dalignment/pose’ and ‘angular direction distribution: azimuth/elevation’. Can any expert help me?
Refined orientations are stored in 3dalignment/pose; they are Rodrigues axis-angle vectors. You can see how they relate to the YZ’Y’’ intrinsic Euler angles that are also used in SPA in the pyem codebase (pyem.geom), and how to compute an angular distribution using these angles in the program star2bild.py.
I’m sure you can also see another way to go directly from axis-angle vectors to viewing directions in spherical coordinates if you read about the axis-angle convention!
Thank you very much! You are right. I have done more classifications and refinements and improved the resolution of the map.
By the way, I have looked through the geom.py on your main page of github. I am a beginner of cryo-EM data processing. The Rodrigues rotation formula: v_rot=v+(sinθ)Kv+(1−cosθ)K^2v. In my opinion, there should be 4 variables in 3-dimension zone: x, y, z(the vector of K), θ. I didn’t know how ‘alignment3d/pose’ ([a,b,c]) could represent these 4 things. If you have spare time, you might teach me more! Thank you!
The viewing axis unit vector is multiplied by the in-plane rotation angle. Rodrigues vectors thus use a solid ball (3-Ball) as opposed to the 4D spherical surface (4-Sphere) of the quaternions or the strange 3-Torus of the Euler angles. Just look up the Wikipedia article, there is a pretty good explanation there.