Hi all,
I can’t homogeneous refine (looks horrible) classes from heterogeneous refinement even though the classes look great coming out of heterogeneous refinement. Any ideas what could be causing this? attaching the two FSCs for comparison.
NHR:
HR:
Your particles are binned too much. Re-extract with less binning, as you are hitting Nyquist. Heterogeneous refinement interpolates (by default) to a 128px box, which in this case I guess is larger than your binned particle size.
Interesting, I’ve never considered this before, does heterogeneous refinement really interpolate to upscale to the given box size rather than zeropad in Fourier space? Wouldn’t the FSC then look different, either reaching an asymptote beyond the particle nyquist or showing a periodic pattern? Either way that sounds very misleading…
EDIT: I should check myself here - zeropadding would exactly be interpolating, but I don’t see how that would lead to a sinusoidal decrease in correlation beyond the data nyquist.
Thanks Oli, I should have noticed there was something different when X-axis extended all the way to unbinned Nyquist for heterogeneous refinement.
Follow-up: in relion this binning still works despite hitting Nyquist, any idea what’s different about the algorithms?
What do you mean by “still works”?
I would be careful to only look at the unsharpened map - the B-factor estimation often goes bananas with binned data.
In relion I can run 3D refinement to Nyquist (bin by 4) followed by 3D classification without alignment to sort out heterogeneity. The 3D refinement still yields reconstructions with secondary structure. In cryosparc homogeneous refinement at bin by 4 doesn’t yield a useful reconstruction.
Edit: yes, only using unsharpened maps, can still see helices (sausages).
Looking at the FSC it still seems to be going to Nyquist though, so I would expect there to still be secondary structural information, unless mask-edge artefacts are dominating. If that is the case, then I would refine without a mask (switching off dynamic masking).
EDIT: Ah just saw your edit. In that case, it might be worth comparing the relion and cryosparc reconstructions using the same B-factor (or no sharpening.
I tried no masking and also changing the resolution at which masking begins to a few different values, no luck. 2D and heterogeneous refinement did work at bin 4, so it wasn’t a waste of time. I’ll re-extract to bin 2 as you suggested for homogeneous and 3D classification, should do the trick.
Thanks!
@au583982 Volumes are zero-padded in real space - it only increases the spectral resolution, which makes peak localization somewhat more robust and decreases interpolation errors in Fourier space.
Doing a reconstruction into a larger (finer) box than the particle box indeed interpolates onto an upsampled grid. The FSC curve will continue past the “real” Nyquist because of 1) structures are smooth in Fourier space and 2) systematic interpolation error will be in common between the half-maps. I don’t think it really causes (additional) over-refinement because the refinement limit in heterogeneous refinement will still effectively be Nyquist, which it would have been anyway.
Okay, so it makes sense that the padding is in real space, but as you say that increases sampling rate in Fourier space with unchanged Nyquist. So why would you then not just reconstruct into the particle box size after alignment? That would be most simple and also give you a true GS-FSC, which would be most transparent, right? I also don’t see how the FSC would obtain that shape beyond the particle Nyquist without applying some exotic heuristics to extend the volume in Fourier space. Simply zeropadding - if you insisted on upsampling - would surely give rise to a high asymptotic FSC beyond the particle Nyquist, as you see when calculating the FSC for globally filtered volumes. I agree that it can’t really lead to overrefinement when the FSC is high even at the particle Nyquist because there’s simply nothing added to overrefine against, but it still seems unnecessarily misleading.
So why would you then not just reconstruct into the particle box size after alignment?
Performance / computational expense - and the size of the class volumes determines the maximum number of classes in a given amount of memory. I do recommend changing the box size to the particle box or a larger fraction of the particle box, especially if you want higher resolution separation.
A true GS-FSC
There’s actually no current software package that does independent half-set refinement in 3D classification. In cryoSPARC the FSC is a simple (non “GS”) half-map comparison, in Relion it is estimated based on a different power spectrum criterion. Thus overfitting is very possible with global search during 3D classification.
(Note Frealign/cisTEM uses a different approach called resolution limited refinement to avoid overfitting, and always considers the entire particle set together - in that case overfitting is prevented simply by choosing a reasonable refinement limit).
I also don’t see how the FSC would obtain that shape beyond the particle Nyquist without applying some exotic heuristics to extend the volume in Fourier space.
If the (non GS) FSC is hitting Nyquist, extending it is just going to create a “normal” looking FSC decay, because the correlated interpolation errors also decay with resolution. There’s nothing exotic - it’s just what happens if you do trilinear interpolation onto a finer grid.
Imagine you upsample a natural image with a sinc interpolator, and there are real space ripples at edge features due to interpolation error. If you had two noisy copies of the images and performed the operation on both of them, they would have similar looking ripples in the same places, despite the independent noise - thus the extra correlations.
a high asymptotic FSC beyond the particle Nyquist, as you see when calculating the FSC for globally filtered volumes
Not sure what you mean. The spurious correlations decay with resolution because the interpolation errors have a certain frequency content dependent on the frequency content of the input, so it’s not a step function. A pair of filtered volumes would have a FSC decay shaped like the edge of the filter window, usually a part of a sinusoid or a Gaussian or Butterworth.
Thanks a lot for the detailed answers, Daniel, they have really helped me a lot to understand some things I’ve never thought about before!
Still some things I’m not sure about:
And regarding the FSC for filtered volumes that I mentioned, this is based on experience in 3DFSC with filtered volumes from CS, which show positive asymptotes after the cut-off resolution. However, I suppose this might be due to improper treatment of the very small fourier amplitudes that may show spurious correlation because of the poor numerical resolution of very small numbers represented as floats.
Sincerely, Martin
Glad my comments were helpful! Continue to call out anything that seems wrong or confusing, as you have been! 
Still, however, I’m not sure why you would want to interpolate to the given box size after reconstruction of each class. Wouldn’t it be both faster and less misleading to simply reconstruct at the particle box size?
Sorry I didn’t say this explicitly before. There is no interpolation after doing a reconstruction. The interpolation takes place during the reconstruction itself. One pixel from a particle image has the coordinates (x, y, 0). This is multiplied by the rotation matrix R for that particle, to find (x’, y’, z’) where to insert into the reconstruction. As x’, y’, z’ are (very likely) noninteger values, we’ll actually look at the rounded down int(x’) and int(x’) + 1, etc. voxels in order to do our interpolations.
If the reconstruction is not the same size as the particle, then we can simply multiply R by the ratio of the sizes (scaling factor) before transforming the coordinates. This same scaling factor also accounts for the change in size due to any zero-padding.
I think we should look more closely and try to figure out whether the inflated FSC really comes from interpolation error or from (Fourier space) smoothness. If it’s the latter, then the FSC isn’t really wrong, but rather the object is just predictable. If it’s the former then the default could perhaps be changed to min(box, 128) instead of 128.
By a non-GS FSC do you mean that the particles are refined together and after refinement simply split into two half-sets, and the half-maps compared?
Correct. I think the original reason not to split half-sets in 3D classification was to keep the effective number of particles larger so as not to miss small classes. FYI Relion doesn’t do this - instead it uses an (also unreliable) SSNR measure to estimate class resolution. You might also be able to turn on half-sets in Relion Class3D using a command line flag (I forget the name, it’s always output by Refine3D).
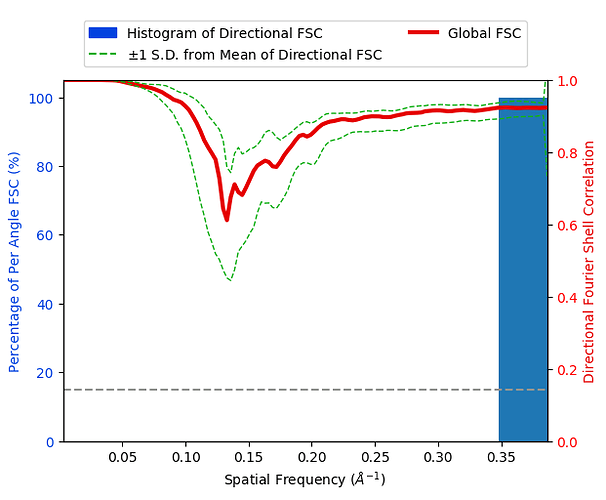
positive asymptotes after the cut-off resolution.
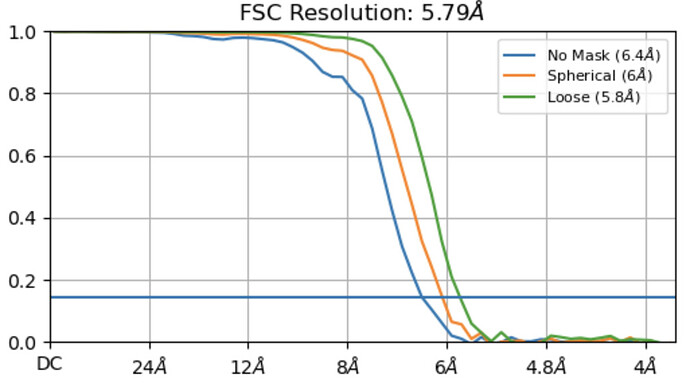
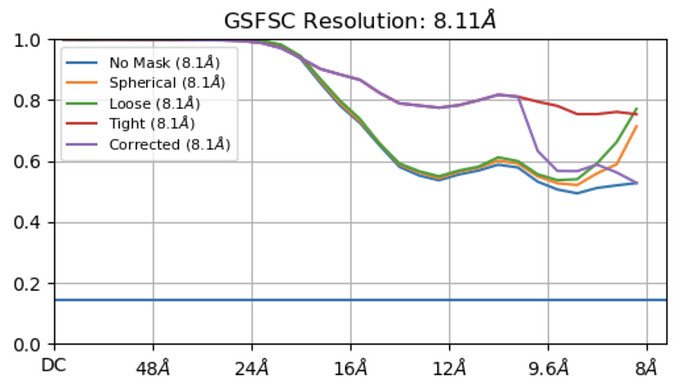
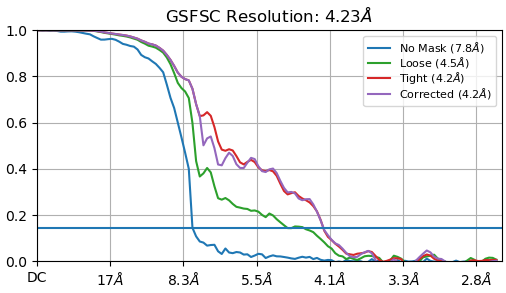
You mean it doesn’t go to zero? Or the curve is step-like? Could you show a picture of what you mean?
Great! Things are starting to make sense. However, I’m still uncertain about which version of the volume that is being used to determine how well each particle fits into each class - the volume that is zero-padded in real space, or the real-space interpolated volume (which should correspond to a volume zero-padded in Fourier space)?
Also, I understand the idea of smoothness in Fourier space when zero-padding in real space - a strong amplitude will be split smoothly across its neighbours. For real-space interpolation, however, this can be achieved by zero-padding in Fourier space, and so I would expect exactly that to be the result. In this case, smoothness should not appear in the extended Fourier space, right?
I can show an example, but I guess it’s due to some incorrect treatment of very small amplitudes when calculating the FSC, so I don’t know how interesting it actually is. If I recall correctly, I had an issue with severe anisotropy due to preferred orientation, which did not show in my FSC from local refinement:
So I thought, why not try to low-pass filter the map to 8 Å to see if it looked more isotropic. After low-passing the half-maps and submitting them to 3DFSC, I got the following:
So this is what I thought of when I wrote “positive asymptote”.
Sincerely, Martin
However, I’m still uncertain about which version of the volume that is being used to determine how well each particle fits into each class
I imagine the algorithm is something like this:
After prepping the 3D FT of the input volume, we only go back to real space to generate outputs for visualization.
I can show an example…
OK, I see what you mean. I agree this could be from dividing by very small numbers outside/at the edge of the filter window, dependent on the exact implementation of filter and FSC steps. The Nyquist limited FSC curves from refinements with a smaller box size are different, though, they look flat out to the end of the plot because they are stretched out (the right edge of the plot is Nyquist).
Try a post processing job on these filtered half-maps, the FSC may be implemented differently than in 3DFSC.
Even though some of the steps are not perfectly clear to me yet, I think that’s something I need to delve into on my own time. Thanks a bunch for all the explanations, Daniel, it’s been extremely informative!
Sincerely, Martin
