Hi @Giovanni! This is a good question, and gets into some tricky problems that come up when working in the discrete world of computers. I think the most likely explanation here is that you’re observing interpolation artifacts.
What really is a cryoEM map
You are likely already familiar with some of the concepts I describe here, but I will provide detail just to ensure we have some shared terminology for these concepts.
First, let’s talk about what we’re looking at when we view a map in a program like ChimeraX. The map itself is a 3D array of real numbers. Each position in the 3D array is called a voxel, and the number stored in the voxel is often informally called “density” (this is not formally correct, as electrons are scattered by Coulomb potential). There are two important things to note here:
- This is a 4D object (three spatial dimensions, one dimension for the value in each voxel), which we of course don’t have a great way to display on a 2D screen
- The voxels are discretely sampled — each voxel represents a cube with side length equal to your pixel size. In real life, proteins are not made of cubes!
To overcome the first problem, we can display a surface which we expect to have the same potential. When you set your threshold in a program like ChimeraX, you’re essentially displaying a surface which encloses voxels which have a value of at least the chosen threshold.
However, when we display this surface, we want it to be visible throughout the entire box, but our data only tells us about the average potential in each voxel. We therefore perform interpolation to model how the Coulomb potential varies as we move between voxels.
Interpolation and symmetry
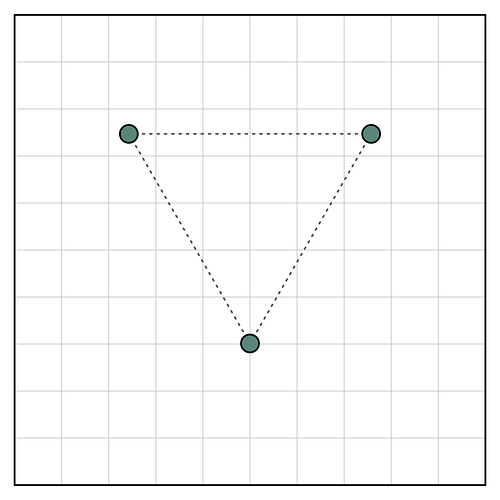
Interpolation is necessary, and typically not noticeable in single-particle data. However, in your case of a high-resolution (congratulations!) reconstruction of a C3 symmetric particle, it is not too surprising that the map is not perfectly symmetric. Consider a simple 2D example:
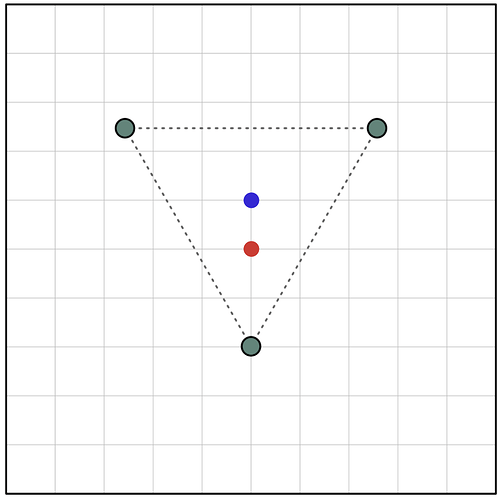
Here I’ve put a C3 symmetric object on a grid of underlying pixels. You can see that two of the three symmetric points are fully contained within a single pixel, but one is split between several. Thus, when we represent this object using the underlying pixel grid, the C3 symmetry is broken:
I’ve obviously created a worst-possible-case example here to emphasize the effect — we generally look at maps with features much greater in size than a single pixel. But hopefully this helps explain why CryoEM maps in general are not perfectly symmetric even when such symmetry is enforced, especially once you consider features at or near Nyquist.