Hi,
I am finding it difficult to understand how to perform symmetry expansion and refinement with symmetry enforced. I am using cryosparc version 3.2
My protein is a homodimer which I’ve refined to 3.7A in cryosparc using local refinement with C1 symmetry. What would be the correct procedure for refinement in C2?
I am trying this but don’t know if it’s correct:
-
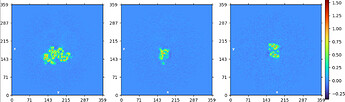
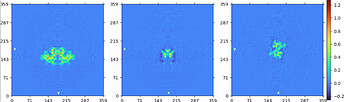
take volume (oriented by eye in Chimera and resampled to lie with symmetry axis along z-axis) and particles from local refine output and run NU refine with C2 enforced and align symmetry enabled - this gave a map that was used to further align along the symmetry axis
input to NU (aligned by eye):
intermediate output of NU:
-
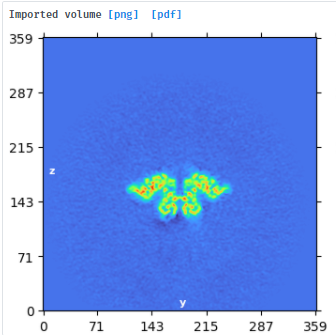
opened output map from step1 in Chimera (#0) - oriented to look down z-axis. Also opened C1 local refine output map (#1), duplicated it (#2), activated map #2 only, then moved/rotated map #2 to fit into map #0 and resampled (vop resample #2 ongrid #1) - saved resampled map and imported to cryosparc
-
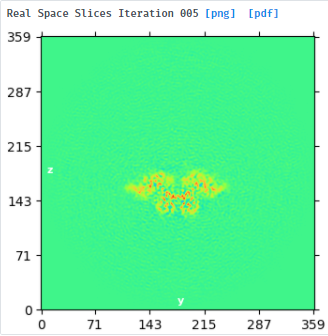
ran NU refine using C1 local refine output particles (not symmetry expanded) with resampled map from step2 as reference volume lowpassed to 10A and C2 symmetry enforced with align symmetry disabled
-
I am planning to then take the output particles from C2 NU refine and run symmetry expansion in C2 (since the particles should now lie at the symmetry axis as far as I understand) before running localrefine in C2 with the expanded particles as input, force-redo split off, small searches with gaussian prior enabled, and reference volume from C2 NU refine (step3) lowpass filtered to just above global resolution
Again, no idea if this is correct so I would appreciate any advice!
Dear @lizellelubbe,
After taking the initial protein from local refinement in C1, you would just need to make sure that it is aligned such that the z-axis is the symmetry axis, before starting a symmetric refinement, as you did in step 1 using Chimera.
Do you see any difference from the output map in step 3 vs. in step 1? If I’m following correctly, the particles are the same and they are both C2 NU-refinements, so the only difference would be the initial volume, which is lowpassed anyway.
The most important considerations to keep in mind when using symmetry expansion are that
- The input particles must already be aligned to the symmetry axes (as done here!)
- Any subsequent local refinements should have C1 as the symmetry value, since the symmetry is already accounted for during the expansion
Symmetry expansion in combination with local refinement is primarily useful when there’s flexibility between each of the asymmetric units. You could try step 4 with expanded particles, running it once with a global mask, and once with a mask over just the asymmetric unit. This may help gauge if accounting for that flexibility is actually helpful.
Best,
Michael
1 Like
Hi @mmclean
Thanks for the very helpful reply! I think I understand it better now.
With step 1 above, I ran NUR in C2 using the reference that was only sort of aligned on the z-axis by eye so the result didn’t really correspond to my protein structure. When I then used that to again align the volume and resample in Chimera it gave me much better results.
I have now done local refine (C2) using the C1 NUR result as input and got 3.7A res so no improvement over the C1 refinement - when would you expect an improvement with symmetry enforced without particle expansion? Local refine after symmetry expansion also did not improve the resolution but I think it may have improved the 3DVA results. Do I understand correctly that symmetry expansion before 3DVA could help since it then captures all/more states for each ASU? There does seem to be flexibility at the dimerization interface along with pronounced opening and closing of a deep cleft in each ASU. I am doing local refine now with a mask around a single ASU on the expanded stack. Is this normally done without particle subtraction?
Hi @lizellelubbe,
Thank you for the clarification above. 3D Variability is internally agnostic to any symmetry in the dataset, which is why symmetry expansion before 3DVA is the recommended way to deal with a symmetric particle (see linked excerpt on symmetry in 3DVA). This will effectively boost the amount of signal that the algorithm can use to fit the variability modes.
The only difference between enforcing symmetry during local refinement, and using symmetry expansion instead, is that the former enforces perfect symmetry whereas the latter allows each expanded image to align independently. So for e.g. enforcing C2 symmetry means the output map will have perfect 180º rotational symmetry, whereas with expanded particles, this is not guaranteed and it’s possible to improve resolution if there is flexibility. This is theoretical though, and if you don’t actually see a resolution/map quality improvement, there could be one of many other factors responsible for limiting the resolution of your map. From our observations/experimentation, signal subtraction doesn’t seem to have a consistent positive or negative effect on the outcome of the map, so it’s hard to predict in advance the effect it will have.
Best,
Michael
3 Likes
Hi @mmclean
Thanks for a very clear and helpful response, as always! It makes a lot of sense