Split output for symmetry expansion

[DanielAsarnow]

Would it be possible to add a “split output” selector for the symmetry expansion job?

This idea is related to but distinct from reversing the expansion. For example, I have a flexible dimer, where I can use subtraction and local refinement to get nice structures of either monomer, and I would like to C2 transform one of these refinements in order to do a single, expanded local refinement with all of the subparticles. One can export the particles and use pyem subparticles.py, but I thought a “split output” feature would be pretty easy to implement and potentially useful for certain classification strategies as well.

[mmclean]

Hi @DanielAsarnow,

Thanks for the post. To clarify, are you referring to splitting the output by which symmetry operator was applied (e.g. so for a C2 expansion, two particle stacks should be outputted, the first corresponding to the identity operation and the second corresponding to a 180º rotation)? This makes sense, however if you wanted to do a single local refinement with all the sub-particles, wouldn’t you need to merge these two stacks immediately before the refinement? Are there other workflows that would specifically benefit from having each set of transformed particles separated?

Currently, separating particles by symmetry transformation should be possible with the data stored in the particle dataset – the sym_expand/idx field will contain the identity of each rotation applied. (An idx of 0 corresponds to the identity transformation, the others are not in any well-defined order).

Best,
Michael

[olibclarke]

Related to this - is there a straightforward way to identify how many “copies” of a given particle are present in a particular class?

Let’s say in @DanielAsarnow’s example of a dimer, there is something binding to each monomer with partial occupancy. in that case we have dimers with 0, 1, and 2 monomers in the bound configuration.

Is there an easy way to separate out these states after symmetry expansion and classification?

With remove duplicates I can separate 1 vs 2 - but what about higher order oligomers? E.g. for a hexamer, how would I identify which particles have all six protomers in the bound configuration?

Cheers
Oli

[mmclean]

Hi @olibclarke,

Interesting question – not sure if this answers it cleanly, but just some thoughts for discussion!

In the case of a dimer, would you use something like:

1. Align all particles to a global C2 reference
2. Symmetry expand in C2
3. 3D classification with mask over both of the sites where there’s partial occupancy

If it works well, you get 3 classes with 0, 1, and 2 binding partners attached (this is like the 3D classification tutorial for empiar-10425). Then you take particles from each class, use remove duplicates to get rid of symmetry-expanded copies.

In principle this could work with higher-order oligomers, but the number of classes that could exist grows exponentially. For N asymmetric units with binding sites, the binding partners could either be present in that site, or absent from that site. So there are two possible states for each ASU, and the total number of configurations is then 2^N (we have to consider each site as being distinct, since we are using symmetry-expanded particles, so fixed-pose classification can/will find different classes as rotated copies of other classes). E.g. for a dimer you have 2^2 = 4 possibilities (bound-bound, bound-unbound, unbound-bound, or unbound-unbound). For a trimer, you have 2^3 = 8, and so on. So for a hexamer, in principle you could do a 64 class 3D classification on C6-symmetry expanded and hope to see classes corresponding to at least some of those 64 configurations.

You can instead put a mask on just one monomer’s binding site, but then you reduce the chances of finding classes with >1 binding partner attached, because the classification masks out everything but one monomer – it can’t look at coordination across different monomers.

Does this make sense / is it in-line with what you’re thinking?

Best,
Michael

[olibclarke]

Hi Michael,

I would generally just mask a single monomer after symmetry expansion.

What I would like to be able to do then, is to identify, for a given particle (i.e. a given location on the micrograph), how many “particles” (original and rotated copies) are retained after classification.

This would avoid the exploding number of classes required for 3D classification in such an instance, and allow a more focused look at the particles that only have, for example, 4/6 sites in a hexamer occupied.

Does that make sense? There is a way to do this with a combination of Particle Sets operations right now, but it is rather convoluted and confusing.

Cheers
Oli

[mmclean]

Ahh this makes sense, thanks @olibclarke for clarifying further.

I imagine this would be possible with the associated metadata in the sym_expand and alignments_class3D_x fields. In this case, an input classification with 2 classes would be needed, one corresponding to the occupied and the other to the unoccupied state. Most likely we could consider adding an example script under the CryoSPARC Tools documentation, since there’s a lot of customizability with this sort of “advanced case” of symmetry-expansion reversal that would make a general implementation in CryoSPARC a bit complex.

Just a few more questions to best understand the utility of such a workflow…

For a symmetry group of order N, would simply identifying & outputting subsets of the symmetry-expanded stack with k/N sites occupied be sufficient? E.g. if you wanted to take a hexamer, and after symmetry expansion & classification break it into 7 disjoint subsets where each subset had either 0, 1, 2, … 6 monomers attached. What would the intended downstream use for these subsets – potentially further classification or refinement?

You can imagine that for 4 of 6 sites occupied, there’s 3 different global configurations possible depending on the relative positions of the occupied/unoccupied sites, so even after identifying that subset, you’d still need more classification at the global-mask level to tease out different states. (This isn’t necessary for the 0, 1, 5, or 6 monomer attached cases, since each of these only has one global configuration, arbitrary up to an overall rotation).

Best, Michael

[olibclarke]

Hi Michael,

For a symmetry group of order N, would simply identifying & outputting subsets of the symmetry-expanded stack with k/N sites occupied be sufficient? E.g. if you wanted to take a hexamer, and after symmetry expansion & classification break it into 7 disjoint subsets where each subset had either 0, 1, 2, … 6 monomers attached. What would the intended downstream use for these subsets – potentially further classification or refinement?

Yep exactly. And quantification/comparison between different datasets. And yes that would be great! Yes the idea is to be able to tease out some context - if we can identify (locally, after sym expansion), which particles have N subunits occupied, and then perform the global classification without alignments just on that subset, that makes the classification significantly less complex.

You can imagine that for 4 of 6 sites occupied, there’s 3 different global configurations possible depending on the relative positions of the occupied/unoccupied sites, so even after identifying that subset, you’d still need more classification at the global-mask level to tease out different states. (This isn’t necessary for the 0, 1, 5, or 6 monomer attached cases, since each of these only has one global configuration, arbitrary up to an overall rotation).

Yes, that’s right, that’s the idea!

Cheers
Oli

[olibclarke]

Hi Michael - was there an easy answer to this in the end? Basically to select a particle subset based on how many symmetry expanded copies there are per particle - e.g., lets say we perform C4 symmetry expansion, and mask around an asymmetric binding site - how to then identify which particles have 1,2,3 or 4 copies in a given (bound/unbound) class?

In theory one could do it with remove duplicates, if there was a concept of occupancy in remove duplicates (instead of just removing duplicates, assign as a 3xduplicate, 4xduplicate, etc). This could also be helpful for selecting a consensus set of particles when using multiple picking approaches (e.g to select only those particles picked in three independent particle sets).

[rwaldo]

Hi @olibclarke! Would something like what’s done in this example achieve what you’re looking for?

Or, if you’re always thresholding on a simple count, you could use CryoSPARC tools and python’s built in Counter like so:

from cryosparc.tools import CryoSPARC
import json
from pathlib import Path
from collections import Counter

with open(Path('~/instance-info.json').expanduser(), 'r') as f:
    instance_info = json.load(f)

cs = CryoSPARC(**instance_info)
assert cs.test_connection()

project_number = "P294"
workspace_number = "W2"
job_number = "J77"

project = cs.find_project(project_number)
job = project.find_job(job_number)
results = job.load_output("split_0")

counted_src_uids = Counter(results['sym_expand/src_uid'])
threshold = 7
# only keep particles if their src_uid appears at least {threshold} times
filtered_src_uids = [
    src_uid
    for src_uid, count in counted_src_uids.items()
    if count >= threshold
]

# this is all the expanded pseudoparticles
filtered_dataset = results.query({
    "sym_expand/src_uid": filtered_src_uids
})

And then, if you just want one entry per symmetry-expanded particle, you could use a normal remove duplicates job on the result.

[olibclarke]

Perfect, thanks Rich I think this should do the trick! I guess if you wanted an occupancy of exactly seven in this case, you would just change if count >= threshold to if count == threshold. That should do it!

[rwaldo]

Yes, that’s right! And I forgot to give my usual caveat that I tested this only by creating random subsets of a symmetry-expanded particle stack and getting a count of particles with at least N in the subset that “felt right”.

I can’t think of any ways this wouldn’t work, but if you get strange results please let me know!

[olibclarke]

Hi Rich - one query - in the script, you have specified the input results as “split_0”. Presumably this is if the input is a particle sets job. If the input is a local refinement job, with outputs as follows, what should this be? I have tried J732.particles.blob and particle.blob without success. Apologies for the silly/basic question, I am probably doing something stupid

Example command and output:

python split_by_symm.py
Connection succeeded to CryoSPARC command_core at http://localhost:39002
Connection succeeded to CryoSPARC command_vis at http://localhost:39003
Connection succeeded to CryoSPARC command_rtp at http://localhost:39005
Traceback (most recent call last):
  File "split_by_symm.py", line 18, in <module>
    results = job.load_output("J732.particles.blob")
  File "/home/user/.local/lib/python3.8/site-packages/cryosparc/job.py", line 413, in load_output
    raise TypeError(f"Job {self.project_uid}-{self.uid} does not have any results for output {name}")
TypeError: Job P48-J732 does not have any results for output J732.particles.blob

[rwaldo]

Not stupid at all!

You’re looking for the string that describes the entire output group, which comprises multiple fields. In the case of your example, the string you want is "particles". I typically look in the smaller output sidebar of the Event Log to avoid the distraction (see images) .

In this case, the string is "particles"

In this case, the string is "particles_class_0"

In this case, the string is "particles_all_classes"

I hope that’s clearer!

[olibclarke]

Ah, gotcha, thanks! Ok that ran without an error, but does not seem to generate any output. Do I need to add a “save external result” section to send the outputs to a job in cryosparc?

[rwaldo]

Yes, apologies. Something like

project.save_external_result(
    workspace_uid=workspace_number,
    dataset=filtered_dataset,
    type="particle",
    passthrough=(job_number, "particles"),
    title=f"Keep particles with {threshold} copies"
)

ought to work.

[olibclarke]

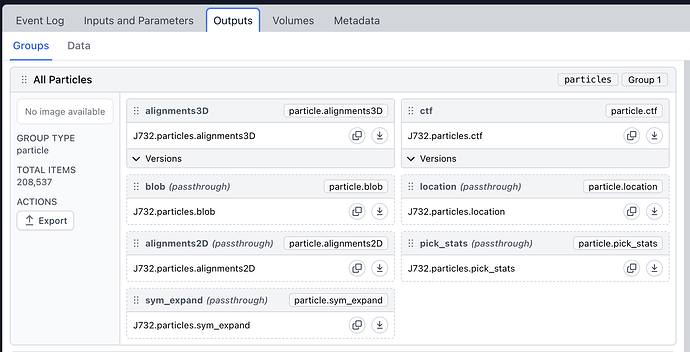
Tried this, but when I run it I get this error:

*** CommandClient: (http://localhost:39003/external/projects/P48/jobs/J745/outputs/particle/dataset) HTTP Error 422 UNPROCESSABLE ENTITY; please check cryosparcm log command_vis for additional information.
Response from server: b'Invalid dataset stream'
Traceback (most recent call last):
  File "split_by_symm.py", line 35, in <module>
    project.save_external_result(
  File "/home/user/.local/lib/python3.8/site-packages/cryosparc/project.py", line 278, in save_external_result
    return self.cs.save_external_result(
  File "/home/user/.local/lib/python3.8/site-packages/cryosparc/tools.py", line 501, in save_external_result
    job.save_output(output, dataset)
  File "/home/user/.local/lib/python3.8/site-packages/cryosparc/job.py", line 1323, in save_output
    with make_request(self.cs.vis, url=url, data=dataset.stream()) as res:
  File "/home/user/software/miniconda3/envs/cryosparc-tools/lib/python3.8/contextlib.py", line 113, in __enter__
    return next(self.gen)
  File "/home/user/.local/lib/python3.8/site-packages/cryosparc/command.py", line 192, in make_request
    raise CommandClient.Error(client, error_reason, url=url)
cryosparc.command.Error: *** CommandClient: (http://localhost:39003/external/projects/P48/jobs/J745/outputs/particle/dataset) HTTP Error 422 UNPROCESSABLE ENTITY; please check cryosparcm log command_vis for additional information.
Response from server: b'Invalid dataset stream'

When I just print(filtered_dataset) the output looks sensible, so I think something is going wrong in the saving of external results - this is using Python 3.8.19, and CS4.4.0

log of command_vis:

2024-03-25 16:00:47,347 request_handler      INFO     | Received request for get_project_file
2024-03-25 16:00:47,384 request_handler      INFO     | Completed request for get_project_file in 0.04s
2024-03-25 16:00:48,215 request_handler      INFO     | Received request for get_project_file
2024-03-25 16:00:48,258 request_handler      INFO     | Completed request for get_project_file in 0.04s
2024-03-25 16:00:52,565 upload_external_job_output INFO     | Received external job output P48.J747.particle
2024-03-25 16:00:52,762 upload_external_job_output ERROR    | Invalid dataset stream
2024-03-25 16:00:52,762 upload_external_job_output ERROR    | Traceback (most recent call last):
2024-03-25 16:00:52,762 upload_external_job_output ERROR    |   File "/home/user/software/cryosparc/cryosparc2_master/cryosparc_tools/cryosparc/dataset.py", line 559, in load
2024-03-25 16:00:52,762 upload_external_job_output ERROR    |     raise TypeError(f"Could not determine dataset format (prefix is {prefix})")
2024-03-25 16:00:52,762 upload_external_job_output ERROR    | TypeError: Could not determine dataset format (prefix is b'\x94CSDAT')
2024-03-25 16:00:52,762 upload_external_job_output ERROR    |
2024-03-25 16:00:52,762 upload_external_job_output ERROR    | The above exception was the direct cause of the following exception:
2024-03-25 16:00:52,762 upload_external_job_output ERROR    |
2024-03-25 16:00:52,762 upload_external_job_output ERROR    | Traceback (most recent call last):
2024-03-25 16:00:52,762 upload_external_job_output ERROR    |   File "/home/user/software/cryosparc/cryosparc2_master/cryosparc_command/command_vis/snowflake.py", line 395, in upload_external_job_output
2024-03-25 16:00:52,762 upload_external_job_output ERROR    |     dset = Dataset.load(request.stream)
2024-03-25 16:00:52,762 upload_external_job_output ERROR    |   File "/home/user/software/cryosparc/cryosparc2_master/cryosparc_tools/cryosparc/dataset.py", line 592, in load
2024-03-25 16:00:52,762 upload_external_job_output ERROR    |     raise DatasetLoadError(f"Could not load dataset from file {file}") from err
2024-03-25 16:00:52,762 upload_external_job_output ERROR    | cryosparc_tools.cryosparc.errors.DatasetLoadError: Could not load dataset from file <werkzeug.serving.DechunkedInput object at 0x7fdbc5e6ecd0>

EDIT: Figured out the issue - when csparc tool was installed (this morning) as per the guide, I installed it with pip install cryosparc-tools. However, it turns out this installs v4.3, not v4.4. When I install it with pip install cryosparc-tools~=4.4.0, the script now works without a problem. I wonder if it would be worth having an automatic check somewhere for a version mismatch, so this is flagged earlier and in a more obvious way?

[rwaldo]

Is it possible that your CryoSPARC tools installation is out of date? Could you try running (in the relevant environment)

pip install cryosparc-tools~=4.4.0

and re-trying?

EDIT: simultaneous replies haha. And I’ve recorded a feature request for such a check!

[olibclarke]

Thanks Rich - the script works great now! Is it possible to save separate particle outputs in a single job? E.g. if I want to iterate through different threshold values, I can output them as separate jobs - can I instead output them as separate particle sets in the same external job? Also, is it possible to write stuff to the log of the external job? E.g. let’s say I make a histogram of threshold vs particle number - would there be any way to present that in the log of the external job that saves the particle outputs?

EDIT: For my future self , here is the current complete script:

#This cryosparc tools script (credit Rich Posert at Structura) takes a symmetry expanded particle set after classification, and splits it by the number of copies, generating a separate particle set for each.
#!!Edit the project, workspace and job of the input as appropriate!!
#!!The "max" variable should be edited as appropriate, e.g. for a tetramer, set to 4!!
#This script should be run from within a cryosparc tools conda environment, as e.g. "python split_by_symm.py"
#If saving external results fails, check that your cryosparc and cryosparc-tools versions match. If they don't, explicitly specify the version of cryosparc-tools at install,
#e.g.: pip install cryosparc-tools~=4.4.0
from cryosparc.tools import CryoSPARC
import json
from pathlib import Path
from collections import Counter

with open(Path('~/cs_instance_info.json').expanduser(), 'r') as f:
    instance_info = json.load(f)

cs = CryoSPARC(**instance_info)
assert cs.test_connection()

#INPUT PARAMETERS - EDIT THESE!
project_number = "P48"
workspace_number = "W6"
job_number = "J731"
max_copies=4
#END OF INPUT PARAMATERS

project = cs.find_project(project_number)
job = project.find_job(job_number)
results = job.load_output("particles")

counted_src_uids = Counter(results['sym_expand/src_uid'])
for i in range(1,max_copies+1):
  threshold = i
  # only keep particles if their src_uid appears at least {threshold} times
  filtered_src_uids = [
      src_uid
      for src_uid, count in counted_src_uids.items()
      if count == threshold
  ]
  # this is all the expanded pseudoparticles
  filtered_dataset = results.query({
      "sym_expand/src_uid": filtered_src_uids
  })
  print(filtered_dataset)
  project.save_external_result(
      workspace_uid=workspace_number,
      dataset=filtered_dataset,
      type="particle",
      passthrough=(job_number, "particles"),

[rwaldo]

You certainly can! You’ll have to create an external job and add outputs to it one by one, like so:

from cryosparc.tools import CryoSPARC
import json
from pathlib import Path
from collections import Counter

with open(Path('~/instance-info.json').expanduser(), 'r') as f:
    instance_info = json.load(f)

cs = CryoSPARC(**instance_info)
assert cs.test_connection()

project_number = "P294"
workspace_number = "W3"
job_number = "J77"
# change this for other job types
output_name = "split_0"

project = cs.find_project(project_number)
job = project.find_job(job_number)
results = job.load_output(output_name)

counted_src_uids = Counter(results['sym_expand/src_uid'])

def count_threshold(threshold):
    filtered_src_uids = [
        src_uid
        for src_uid, count in counted_src_uids.items()
        if count == threshold
    ]
    filtered_dataset = results.query({
        "sym_expand/src_uid": filtered_src_uids
    })
    return filtered_dataset

thresholded_datasets = {}
# choose your thresholds here
for thresh in range(4,15):
    thresholded_datasets[thresh] = count_threshold(thresh)

# make plot
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize = (8, 3))
ax.bar(
    thresholded_datasets.keys(),
    [len(x) for x in thresholded_datasets.values()]
)
ax.set_ylabel('Number of particles')
ax.set_xlabel('Count threshold')
fig.tight_layout()

out_job = project.create_external_job(
    workspace_uid=workspace_number,
    title=f"Threshold particle counts",
    desc="Each output contains particles with at exactly N copies in input."
)
out_job.add_input(
    type = "particle",
    name = "input_particles"
)
out_job.connect(
    target_input = "input_particles",
    source_job_uid = job_number,
    source_output = output_name
)

for thresh, dset in thresholded_datasets.items():
    output = out_job.add_output(
        type = "particle",
        name = f"threshold_{thresh}",
        passthrough = "input_particles",
        slots = ["blob"],
        alloc = dset
    )
    out_job.save_output(f"threshold_{thresh}", dset)

out_job.log_plot(fig, "Histogram of particles retained at each threshold.")
out_job.stop()

This’ll create a job with a list of outputs, one for each threshold:

and at the end of the log, you’ll see the particle count at each threshold:

[rwaldo]

To save the pain of reading what has become a longer script on the forum, the same code is available as a notebook here: cryosparc-examples/count_sym_exp_copies.ipynb at main · cryoem-uoft/cryosparc-examples · GitHub

That version automatically finds the greatest count and covers the whole range.