Particle sets distance-based selection

Particle Picking
1

Hi all -

I’ve been searching for something like this but haven’t found:

  1. I have two distinct particle sets picked from the same data set, set-A and set-B.
  2. I want to select particles from set-B that are within X distance of the particles in set-A.
    Is there a way to do this?

Thanks,
Owen

2

Use remove duplicates, with the option “remove duplicates entirely” switched on. The removed duplicates (output as a separate subset) will now be the selection you want (assuming there are no duplicates within either set A or set B).

3 Likes
3

Yes, we thought of that but unfortunately it won’t work because the assumption is not correct. There will be set A-set A pairs and set B-set B pairs that will be selected.

To give more context, we are picking particles from within assembled capsids. The idea is that set A defines one part of the capsid, and set B defines another part. We want set A-set B pairs that are within a certain distance of each other.

A solution is to convert them to star files and then do the selection that way, but then we lose some of the metadata (pick stats, etc.) from cryosparc that we’d rather like to keep.

1 Like
4

Ah yes I see what you mean - I don’t think there is a way to do that directly in the GUI, but possibly with cryosparc tools? @rposert?

5

Hi @opornillos and @olibclarke! This is an interesting problem!

Just to make sure I’m following, you have set A and set B, picked from the same micrographs. Your desired result is the set of particles which are in (or, are close to each other in) both A and B, and no other particles.

The problem you note with Oli’s method (remove entirely and use the removed particles) is that the radius you need to use will also create some A/A pairs and B/B pairs, which is undesirable.

If I have all that right, I would definitely reach for CryoSPARC Tools! Here’s an outline of how I might proceed:

First, I’d start with Oli’s method to select particles which are certainly near other particles: that is, all A/A, A/B, and B/B pairs. I would start this way because comparing positions is relatively slow, and this will throw out particles that are definitely not in your final desired set.

Then, working micrograph by micrograph (which you could do using dataset.query() in a for loop over the micrograph UIDs), I would try the following process:

  1. Get the X,Y coordinates for each particle in A. These are found in the fields location/center_{x,y}_frac.
  2. Convert those distances to pixels by multiplying by the relevant location/micrograph_shape values
  3. Do the same for particles in B.
  4. Use scipy.spatial.distance.cdist() to find the pairwise distance between all points in A and all points in B.

Now, you have an MxN matrix, where M and N are the number of particles in A and B. Each entry (i,j) is the distance between the ith particle from A and the jth particle from B. So, you can follow this procedure to keep only the particles that are some minimum distance away from any particle in A:

  1. Iterate over the particles in B, with some index j.
  2. Check the minimum distance of the j-th column in your distance matrix. If it is below your threshold, save the relevant B particle’s UID.

Once that’s done, you’ll have a list of UIDs which belong to B particles that are some distance away from an A particle. With that, a simple query() will get you the set you want, and it can be saved using save_external_job().

Here is some example code starting with a fake list of A and B particle coordinates:

import numpy as np
from scipy.spatial import distance

a_particles = np.array([[0,0],
                        [1,1],
                        [0,2],
                        [1,3]])

b_particles = np.array([[2.0,1.0],
                        [1,0.3],
                        [1.1,3.1]])
distances = distance.cdist(a_particles, b_particles)
maximum_distance = 0.8

for j in range(len(b_particles)):
    nearest_a_distance = np.min(distances[:,j])
    if nearest_a_distance <= maximum_distance:
        print(f'Keep UID {j}')

# output
Keep UID 1
Keep UID 2

And here’s a plot representing, graphically, what we’re doing here. The A particles are black points. The B particles are numbered by their “UID”, and have a green circle with radius maximum_distance. If this radius overlaps a black point, we keep the particle. Otherwise, we discard it.

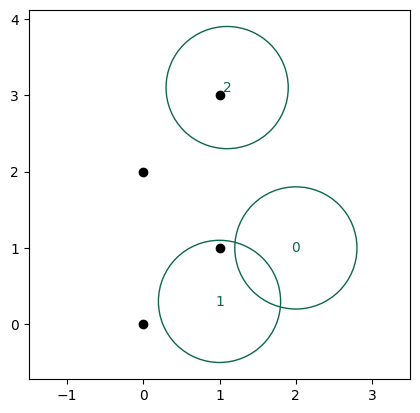
image

You can see that even though B particles 0 and 1 would be counted as duplicates (their circles overlap), we correctly rejected B particle 0 because it is not close enough to any A particle.

I hope that helps!

1 Like
6

Thanks so much! I’m trying to implement this now and will let you know how it goes.

I hope this is something that can be included in the GUI at some point - I can envision a lot of possible uses for it esp. with people picking and solving structures from “non-canonical” particles.