I got a 4-start helix. The global parameters are twist 40 degree, rise 13.82 Angstrom. How do I define the 4-start helix in parameter for symmetry refinement?
Hi @builab,
By 4-start, do you mean that the helix has C4 symmetry around the helical axis? If so, then you can input the global parameters (40º, 13.84 Å) as twist and rise, and set symmetry to C4.
If you mean instead that each of the “starts” is offset from each other, translated along the helical axis by the same amount, I believe Shaoda He & Sjors Scheres’s helical reconstruction paper gives an equation to convert the global parameters to ones suitable for refinement. I believe this figure from the paper illustrates this kind of helix.
Best,
Michael
Oh, I mean the n-start helix with C1. I tried to Shaoda He’s conversion. However, the resolution is decreased not increased. I don’t have this experience so I will play with it a bit more.
Best,
H
Did you try with just the standard params 40º and 13.84Å, and C1 symmetry? I think that would be correct, just would result in less symmetry averaging overall (relative to Shaoda He’s conversion eq.) – but adjacent asymmetric units would still add together coherently as long as each start individually obeys those symmetry parameters.
Best,
Michael
Dear Michael,
It actually works very well. So it is my lack of understanding of helical symmetry. 40, 13.84 & C1 I got 5 Angstrom, change to 40 degree, 13.84Angstrom, C4, I got 4 Angstrom and clearly see the side chain.
first, hi Bui lab !
I hav a similar question. We have tube data which I suspect has multiple starts but we can’t figure out how many, due to the rise being so small and it’s unclear what the ASU is. We have subtomo averaging of the tube, but resolution isn’t great. Given this tube, cryosparc unambiguously finds the symmetry: 4.937A rise and -167 twist. The helcial search job top 10 results all pretty much give the same value, so I’m confident it’s this. However, when I run the refinement in CS or in RELION it gives terrible results. I really don’t get it.
I am wondering if the issue is that I need to use the formula from the Shaoda He paper, or if CS sym search utility already takes this into account. I’m a bit stuck because we seemingly have clear symmetry parameters but it still isn’t working, meanwhile it certainly seems plausible it could have many starts. I’m also not sure how C symmetry comes into play here. My understanding is that, as Builab pointed out, it should run even as C1 but improve with higher C sym. On the other hand, if the # of starts is wrong then it will never even look like a reasonable reconstruction…
thanks!
Hi J,
With the speed of cryosparc, maybe you can do trial & error for C1 to C20 for example? If the entire dataset is problematic due to size, perhaps, use a subset of particles?
hi, that’s a good idea. Thanks.
I guess I was wondering what the relationship is though between C and N-start. I guess there is none. But it seems like there should be.
Hi @orangeboomerang,
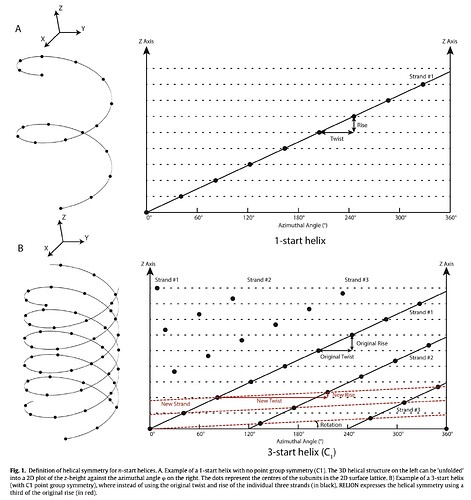
Chiming in a bit late, but I can clarify the difference between “n-start C1 helical symmetry”, and a “n-start Cn helical symmetry”. These are best described by Shaoda He and Sjors Scheres’ Helical reconstruction in RELION. The former (n-start C1 helical symmetry) is shown in Figure 1B:
Figure 1 from Helical Reconstruction in RELION [1]
Note the “offset” positioning of subunits along each of the 3-starts. The conversion equation that converts the symmetry parameters from a “n-start C1” helical filament (i.e. the symmetry parameters that represent any of the black strands in Figure 1B) to a 1-start helical filament is shown later in the paper (on page 165 – unfortunately the equation is unnumbered). To use this symmetry group, CryoSPARC expects the symmetry parameters in the 1-start form, and it expects a C1 point symmetry group.
On the other hand, “n-start Cn” helical filament corresponds to what you’d get by naively applying Cn symmetry to the 1-start strand in Figure 1A. This case can be specified to CryoSPARC as a helical symmetry with an rise and twist, when a Cn group is specified.
Best,
Michael
[1] S. He and S. H. W. Scheres, “Helical Reconstruction in Relion,” Journal of Structural Biology, vol. 198, no. 3, pp. 163–176, 2017. doi:10.1016/j.jsb.2017.02.003