Hi,
The 3D variability analysis is very informative. Regarding the choice of the number of modes to solve - is there any way to quantify the contribution of the relative eigenvectors? That is how much residual variability is explained by for example the fifth eiegenvector? This would be useful for justifying how many modes to analyze for.
Secondly, regarding the parameters - are there any general recommendations regarding tweaking/troubleshooting? E.g. it is mentioned in the tooltip that increasing lambda from the default value of 10 can be helpful to stabilize results if artefacts are observed. What kinds of artefacts are typically observed, and what kind of range should one vary lambda over - e.g. increase to 100? 1000?
Cheers
Oli
Hi @olibclarke,
Good questions - the number of modes in general can be set as high as possible before running into memory errors or “artefacts” (explained below). The algorithm will construct the top-K eigenvectors in terms of their eigenvalues, so theoretically the results of asking for K or K+1 modes will be the same for the first K modes. In practice often multiple modes have very similar eigenvalues and so the order is not always the same (depends on initialization and number of iterations - default 15).
Right now we don’t print out the eigenvalues (which are the actual variance along the direction of each eigenvector) but you can see the “spread” of particles along each direction in the “reaction coordinate” plots. There is an actual quantification possible of the eigenvalues to determine their significance, and that quantification essentially involves comparing the eigenvalues to the estimated noise spectrum of the images, and if the eigenvalue is significantly larger than noise, it is significant. However right now in the first version, we don’t use/compute the noise model so this will be upcoming.
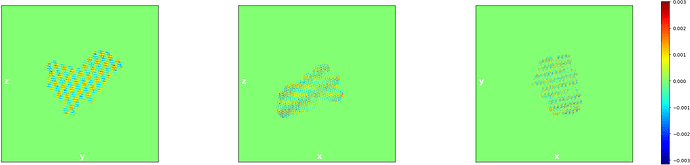
The lambda parameter you mention is a regularizer that theoretically should not be necessary but in practice there seems to sometimes be a numerical stability/precision issue which causes the algorithm to diverge and create artefacts (very obvious streaking - see image) if lambda is not large enough. If you do see this streaking, then lambda should be increased by a fator of 10,100,1000 etc until the streaking is gone. We’re hoping to sort out the root cause of this so that lambda will no longer be needed.
Other parameters I would suggest trying to change are the filtering options - depending on the amount of variability/motion, it’s helpful to filter to around the same resolution as the size of motion. Eg. 5A motion means filter to ~5A. The number of iterations should typically not need to be higher than 15, but may be worth playing with. Masking is by far the most important choice, as the presence/absence of a variable domain within the mask will completely change what the top-K eigenvectors are.
Hope this helps!
Ali
3 Likes
@apunjani The artifacting seems to be affected by the number of basis vectors solved, i.e. no artifacts with lambda 10 and 3 vectors, strong artifacting with lambda 10 and 6 vectors. It could also be the random seed so I’ll run it a couple more times to check.
@DanielAsarnow, which model of GPU and CUDA version are you running?
I have 2x GTX 1080 Ti (11178 MiB) and CUDA 10.1 on CentOS 7.6.
BTW it seems like the random seed doesn’t matter.
Hmm… thanks for letting me know. Any chance you have an older GPU somewhere you could try on, Kepler GPU? (K40 etc)? There’s a chance that newer cc cards have slight difference in the implementation of a particular instruction that causes a numerical instability. I’m investigating here also
Sorry Ali, I didn’t see your post. Unfortunately I only have 1080 Ti and newer cards available.
Hi @apunjani, just want to revisit this - I understand that the modes are ordered in terms of significance, but is there any way to quantify this? E.g. it would be nice to be able to say something along the lines of “the top three modes explained 95% of the residual heterogeneity in class x” - having some justification for the number of modes to analyse would be nice for reporting results if nothing else.
Also, regarding the filter resolution, you say that it is helpful to filter to around the same resolution as the size of the motion - Can you explain this a little more? When you say the size of the motion, do you literally mean displacement of a region by x Å, or is it more akin to “motion that is visible when I filter volumes to x Å”. I would expect intuitively that a small motion of a large domain would still be visible when I filter at say 10 Å, even if the displacement of that domain is only 2 or 3 Å - is this not correct?
Finally, in your webinar you say that you really as a rule of thumb want at least 100k particles for this to work well - is this number dependent upon the size of the particles, or at least the size of the masked region? I would imagine for smaller particles one requires more?
Cheers
Oli
UPDATE:
I see from discussions elsewhere in the forum that quantifying the contributions of the individual components is still a work in progress.
Hi, all. A following up question: do you now implement to output the values of “reaction coordinates” of the volume (of a single particle image), i.e., the fraction of of each eigen-volume of a 3D volume.
Regards,
Ben
Sorry. It’s solved… The value for each component is stored in the .cs file.
Thanks,
Ben