Hi @olibclarke! I’ll answer your question about the plot, and also take advantage of your follow-up to provide a little more detail on the latent spaces. I simplified a lot in my first explanation, so in case anyone else reading wants a little more detail (before I have time to update the guide  ) I’ll include it here.
) I’ll include it here.
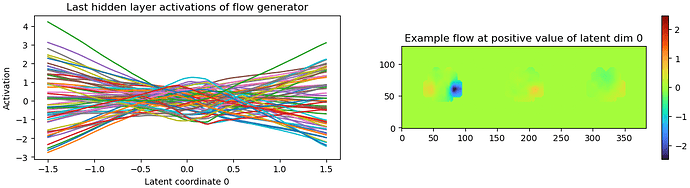
What’s the example flow plot?
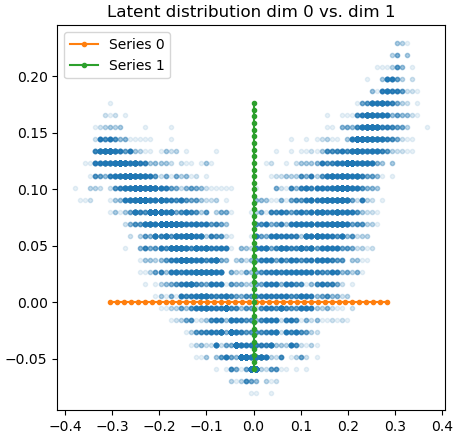
The plot you’re describing is more of a sanity check than something that really tells you important information about your model. The left part just measures the activations — you want this to look “not too flat, not too squiggly”.
The plot on the right looks like a 3DVA plot, but it’s a bit different.
Recall that in 3DVA we’re scaling and adding a “difference volume” to the consensus volume. So we can plot an unscaled difference volume to see what that mode of 3DVA is doing.
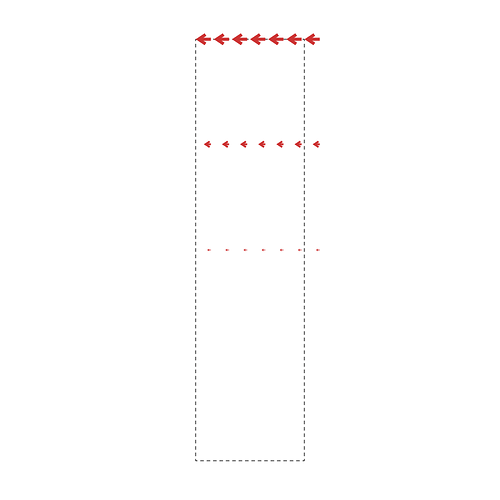
Here, though, we’re moving density around rather than adding and subtracting it. So we need to think about both the three dimensions of the model, plus the three dimensions of the flow field. That’s a bit much for a 2D plot, so same slice of the volume in all three parts of the right-hand plot. Each slice has a different dimension of the flow field plotted on it, with the colors telling us how far the flow field wants to move density from that region. The flow field plotted is taken from the particle with the highest (i.e., furthest) coordinate in latent coordinate 0.
For instance, in the plot above, we see that the particle furthest along component 0 wants to move the density at the right-hand side of this slice in the approximate direction (-2, 0.5, 0.5). It wants to move the left-hand side of the slice in the approximate direction (0.5, 0, 0).
Like the activations, you’re basically looking for “something” here. No color at all means the flow field isn’t moving density anywhere, really noisy colors means density is getting thrown all over the place, which is probably not what’s actually happening to the particles.
I hope that helps explain these plots! Now on to
More on latent spaces
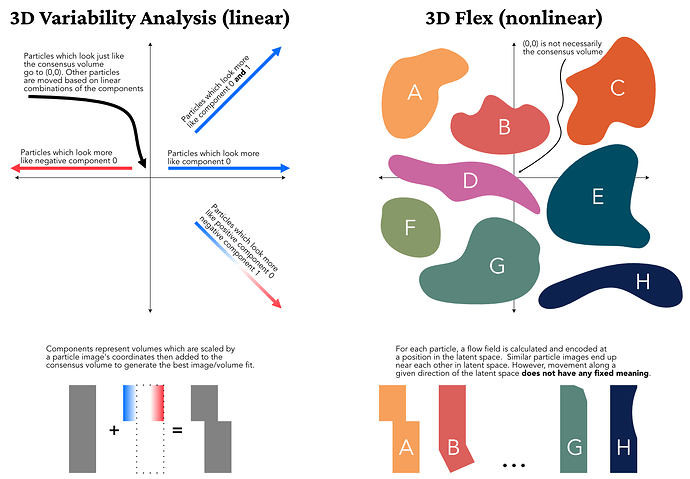
3DVA is linear, so each particle gets placed according to the linear combination of each component which best explains the observed image. When you plug those particles into 3D Flex Train jobs they are assigned that same coordinate position in the latent space, but during training the latent space may expand to incorporate other types of motion. This could in turn move the types of motion modeled by the linear 3DVA functions closer to each other in the highly non-linear latent space.
For a simple example, consider a water molecule’s vibrations: asymmetric stretch, symmetric stretch, and bending. Providing 3DVA with two modes resolves symmetric stretch to component zero and asymmetric stretch to component one. However, 3D Flex also detects bending. Since the latent space is not linear, it can “move” particles from their linear 3DVA coordinates to coordinates which “make room” for the bending motion as well.
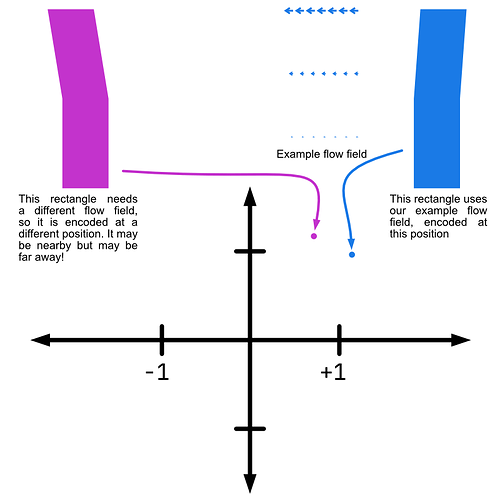
For another way to think about this: a coordinate (a, b) in 3DVA’s coordinate space means “this image is best modeled by multiplying a * V0 and b * V1 and adding the result to the consensus map”. The same coordinate in 3D Flex means “this image is best modeled by deforming the consensus map by the flow field encoded at (a, b)”.
This has a few pretty significant implications. Most importantly, a latent space dimension is very different from a 3DVA dimension. Since 3DVA dimensions are linear, each dimension captures a “type” of conformational change, and a particles coordinate tells you “how much” of each “type” of change that particle has applied to it. This means that you (ideally) need as many coordinates as you have distinct types of motion.
Contrast this with 3D Flex latent space coordinates. I think it is best to think of latent space coordinates as “neighborhoods”. In each region of latent space you have particles which look similar to each other (more precisely: which are best-modeled by similar flow fields). This means that moving along an axis in the latent space is locally defined — the difference between (0.5, 0.0) and (0.6, 0.0) might be (and, indeed, probably is) very different from the difference between (0.5, 1.0) and (0.6, 1.0). This is one of the reasons for noise injection during training — we want to ensure that (a, b) looks similar to (a + e, b + e) for small e, but the model could put dissimilar flows near each other. We thus “blur out” latent space coordinates to ensure the desired local smoothness.
Note also that since the latent space is not a linear span, there is no reason to expect that (0, 0) corresponds to the consensus map. In fact, it is not certain that any coordinate in the latent space will correspond to the consensus map.
This also means you can “fit” far more distinct states in a latent space with two dimensions than you can in a 3DVA coordinate space with only two dimensions. I like to think of dimensions in latent space as describing the greatest number of adjacent neighborhoods the 3D Flex model has access to.
Note that we’re still modeling the same object — it will still have the same degrees of freedom, since that is an intrinsic property of the object. However, 3D Flex’s nonlinearity means we may be able to embed more states of that object in a lower dimensional latent space than 3DVA’s coordinate space. We will not, however, then be able to model the transitions between those states, so the model (and therefore reconstruction) will be incomplete.
For me, at least, latent spaces are very difficult to think about and I constantly find myself falling into the trap of thinking about them as if they are linear. I thus want to add a final way of thinking about latent spaces to this very long post.
I have found visualizations of latent spaces of the MNIST handwritten digits dataset very helpful. I think these give a nice intuitive view of what’s happening in a latent space. For instance, the figure toward the bottom of this article samples the latent space at a fixed interval. We can see that, at high values of z[1], moving along z[0] rotates and morphs the handwritten 0. However, at low z[1], moving along z[0] turns a 7 into a slanted 1 without really rotating the main stroke very much. Similar non-linearity is visible in the z[1] component. (Note that 3D Flex uses an auto-decoder rather than that website’s VAE, but the principle is still similar).